-
Persamaan kuadrat x2 – 5x + 6 = 0 mempunyai akar – akar x1 dan x2. Persamaan kuadrat yang akar – akarnya x1 – 3 dan x2 – 3 adalah …
A. x2 – 2x = 0
B. x2 – 2x + 30 = 0
C. x2 + x = 0
D. x2 + x – 30 = 0
E. x2 + x + 30 = 0
PEMBAHASAN :
akar – akarnya :
x1 – 3 = y  x1 = y + 3
x1 = y + 3
x2 – 3 = y  x2 = y + 3
x2 = y + 3
substitusi nilai “x1” atau “x2” kepersamaan kuadrat dalam soal, sehingga menjadi :
x2 – 5x + 6 = 0
PK Baru : (y + 3)2 – 5(y + 3) + 6 = 0
y2 + 6y + 9 – 5y – 15 + 6 = 0
y2 + y = 0
JAWABAN : C
-
Diketahui sebidang tanah berbentuk persegi panjang luasnya 72 m2. Jika panjangnya tiga kali lebarnya, maka panjang diagonal bidang tersebut adalah … m.
A. 
B. 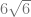
C. 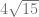
D. 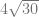
E. 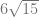
PEMBAHASAN :
p = 3l
p x l = 72
3l x l = 72
4l2 = 72
l2 = 18
l = 
p = 3l = 3. 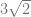 =
= 
Diagonal = 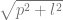
= 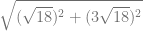
= 
= 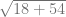
= 
= 
JAWABAN : A
-
Pak Musa mempunyai kebun berbentuk persegi panjang dengan luas 192 m2.
Selisih panjang dan lebarnya adalah 4 m. Apabila disekeliling kebun
dibuat jalan dengan lebar 2 m, maka luas jalan tersebut adalah … m2.
A. 96
B. 128
C. 144
D. 156
E. 168
PEMBAHASAN :
p – l = 4
p x l = 192
(4 + l) x l = 192
4l + l2 = 192
l2 + 4l – 192 = 0
(l – 12)(l + 16) = 0
l = 12 atau l = -16 (tidak memenuhi)
p = 4 + l = 4 + 12 = 16
Untuk menentukan luas jalan, kita partisi-partisi menjadi 8 yaitu :
4 luas jalan yang berada di pojok-pojok kebun berbentuk persegi dengan panjang sisi 2cm : 4 x 22 = 16cm2
2 luas jalan yang berada pada panjang kebun dengan panjang sisi 12cm dan lebar 2cm : 2 x (12 x 2) = 48cm2
2 luas jalan yang berada pada lebar kebun dengan panjang sisi 8cm dan lebar 2cm : 2 x (8 x 2) = 32cm2
Jadi luas jalan yang dibangun adalah 16 + 48 + 32 = 96cm2
JAWABAN : A
-
Diketahui akar – akar persamaan kuadrat 2x2 – 4x + 1 = 0 adalah m dan n. Persamaan kuadrat baru yang akar – akarnya  dan
dan  adalah …
adalah …
A. x2 – 6x + 1 = 0
B. x2 + 6x + 1 = 0
C. x2 – 3x + 1 = 0
D. x2 + 6x – 1 = 0
E. x2 – 8x – 1 = 0
PEMBAHASAN :
y1 + y2 =  +
+ 
= 
= 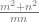
= 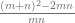
= 
= 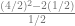
=  = 6
= 6
y1.y2 =  .
.
= 
= 1
PK Baru : y2 – (y1 + y2)y + (y1.y2) = 0
y2 – 6y + 1 = 0
JAWABAN : A
-
Persamaan 2x2 + qx + (q – 1) = 0 mempunyai akar – akar x1 dan x2. Jika x12 + x22 = 4, maka nilai q = …
A. -6 dan 2
B. -6 dan -2
C. -4 dan 4
D. -3 dan 5
E. -2 dan 6
PEMBAHASAN :
x12 + x22 = 4
(x1 + x2)2 – 2x1x2 = 4
(-b/a)2 – 2(c/a) = 4
(-q/2)2 – 2((q – 1)/2) = 4
q2/4 – q + 1 = 4 (kalikan 4)
q2 – 4q + 4 = 16
q2 – 4q – 12 = 0
(q – 6)(q + 2) = 0
q = 6 atau q = -2
JAWABAN : E
-
Jika nilai diskriminan persamaan kuadrat 2x2 – 9x + c = 0 adalah 121, maka c = …
A. -8
B. -5
C. 2
D. 5
E. 8
PEMBAHASAN :
D = 121
b2 – 4ac = 121
(-9)2 – 4(2)(c) = 121
81 – 8c = 121
81 – 121 = 8c
-40 = 8c
-5 = c
JAWABAN : B
-
Persamaan (1 – m)x2 + (8 – 2m)x + 12 = 0 mempunyai akar kembar, maka nilai m = …
A. -2
B. -3/2
C. 0
D. 3/2
E. 2
PEMBAHASAN :
Akar kembar jika D = 0
b2 – 4ac = 0
(8 – 2m)2 – 4(1 – m)(12) = 0
64 – 32m + 4m2 – 48 + 48m = 0
4m2 + 16m + 16 = 0
4(m2 + 4m + 4) = 0
(m + 2)(m + 2) = 0
m1,2 = -2
JAWABAN : A
-
Jika x1 dan x2 adalah akar – akar persamaan kuadrat x2 + px + 1 = 0, maka persamaan kuadrat yang akar – akarnya 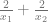 dan x1 + x2 adalah …
dan x1 + x2 adalah …
A. x2 – 2p2x + 3p = 0
B. x2 + 2px + 3p2 = 0
C. x2 + 3px + 2p2 = 0
D. x2 – 3px + 2p2 = 0
E. x2 + p2x + p = 0
PEMBAHASAN :
misal :
y1 = 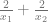
y2 = x1 + x2
y1 + y2 = (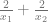 ) + (x1 + x2)
) + (x1 + x2)
= (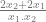 ) + (x1 + x2)
) + (x1 + x2)
= ( ) + (-b/a)
) + (-b/a)
=  + (-b/a)
+ (-b/a)
= 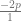 + (-p/1)
+ (-p/1)
= -3p
y1.y2 = (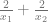 ).(x1 + x2)
).(x1 + x2)
= (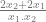 ) + (x1 + x2)
) + (x1 + x2)
= ( ).(-b/a)
).(-b/a)
=  .(-b/a)
.(-b/a)
= 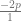 .(-p/1)
.(-p/1)
= 2p2
PK Baru : y2 + (y1 + y2)y + (y1.y2) = 0
y2 + (-3p)y + (2p2) = 0
y2 – 3py + 2p2 = 0
JAWABAN : D
-
Suatu fungsi kuadrat mempunyai nilai minimum –2 untuk x = 3 dan untuk x = 0 nilai fungsi 16. Fungsi kuadrat itu adalah …
A. f(x) = 2x2 – 12x + 16
B. f(x) = x2 + 6x + 8
C. f(x) = 2x2 – 12x – 16
D. f(x) = 2x2 + 12x + 16
E. f(x) = x2 – 6x + 8
PEMBAHASAN :
misal : f(x) = ax2 + bx + c
substitusi x = 0 untuk nilai fungsi 16, sehingga :
f(0) = a(0)2 + b(0) + c
16 = c … (i)
Substitusi x = 3 untuk nilai minimum -2, sehingga :
f(3) = a(3)2 + b(3) + c
-2 = 9a + 3b + c … (ii)
f’(x) = 2ax + b
substitusi titik x = 3 (titik minimum) untuk f’(x) = 0, sehingga :
0 = 2a(3) + b
b = -6a … (iii)
substitusi (i) dan (iii) ke (ii), sehingga diperoleh :
-2 = 9a + 3b + c
-2 = 9a + 3(-6a) + 16
-2 = 9a – 18a + 16
-18 = -9a
2 = a
b = -12
f(x) = ax2 + bx + c
substitusi a = 2 , b = -12 dan c = 16
f(x) = 2x2 – 12x + 16
JAWABAN : A
-
Nilai maksimum dari fungsi f(x) = –2x2 + (k+5)x + 1 – 2k adalah 5. Nilai k yang positif adalah …
A. 5
B. 6
C. 7
D. 8
E. 9
PEMBAHASAN :
f(x) = –2x2 + (k + 5)x + 1 – 2k
f’(x) = -4x + k + 5 = 0
-4x = -(k + 5)
x = (k + 5)/4
substitusi nilai “x” ke fungsi :
f(x) = –2x2 + (k+5)x + 1 – 2k
5 = –2(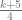 )2 + (k+5)(
)2 + (k+5)(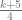 ) + 1 – 2k
) + 1 – 2k
5.16 = -2k2 – 20k – 50 + 4k2 + 40k + 100 + 16 – 32k
80 = 2k2 – 12k + 66
2k2 – 12k – 14 = 0
2(k2 – 6k – 7) = 0
2(k – 7)(k + 1) = 0
k = 7 atau k = -1
JAWABAN : C
-
Absis titk balik grafik fungsi f(x) = px2 + ( p – 3 )x + 2 adalah p. Nilai p = …
A. -3
B. -3/2
C. -1
D. 2/3
E. 3
PEMBAHASAN :
Titik balik = titik minimum.
f(x) = px2 + ( p – 3 )x + 2
f’(x) = 2px + p – 3 = 0
substitusi x = p, sehingga diperoleh :
2p2 + p – 3 = 0
(2p + 3)(p – 1) = 0
p = -3/2 atau p = 1
JAWABAN : B
x1 = y + 3
x2 = y + 3
=
dan
adalah …
+
= 6
.
dan x1 + x2 adalah …
) + (x1 + x2)
) + (x1 + x2)
) + (-b/a)
+ (-b/a)
+ (-p/1)
).(x1 + x2)
) + (x1 + x2)
).(-b/a)
.(-b/a)
.(-p/1)
)2 + (k+5)(
) + 1 – 2k
) + 4(
) +
2 komentar:
mas dah mangstab neh blognya...jangan lupa koment balik di
http://sandikupep.blogspot.com/
ok deh....tp kayak na belum puas aku mas.....heheheheheheheehhe
Posting Komentar